Уже довольно давно мы советуем использовать вычисления с плавающей точкой в реализациях демозаики (байеровской интерполяции), что позволяет получить существенно лучшие результаты.
Кстати, некоторые разработчики, которые ранее активно настаивали на том, что точности целых вычислений достаточно, в настоящее время свои алгоритмы интерполяции реализуют в плавающей точке.
Вот сравнение результатов AHD-демозаики, реализованных по одному и тому же алгоритму, но с разной точностью вычислений: с плавающей точкой и тот же самый алгоритм, но в целых числах (оригинальный код из dcraw).
| Неразмытая мишень | |
|---|---|
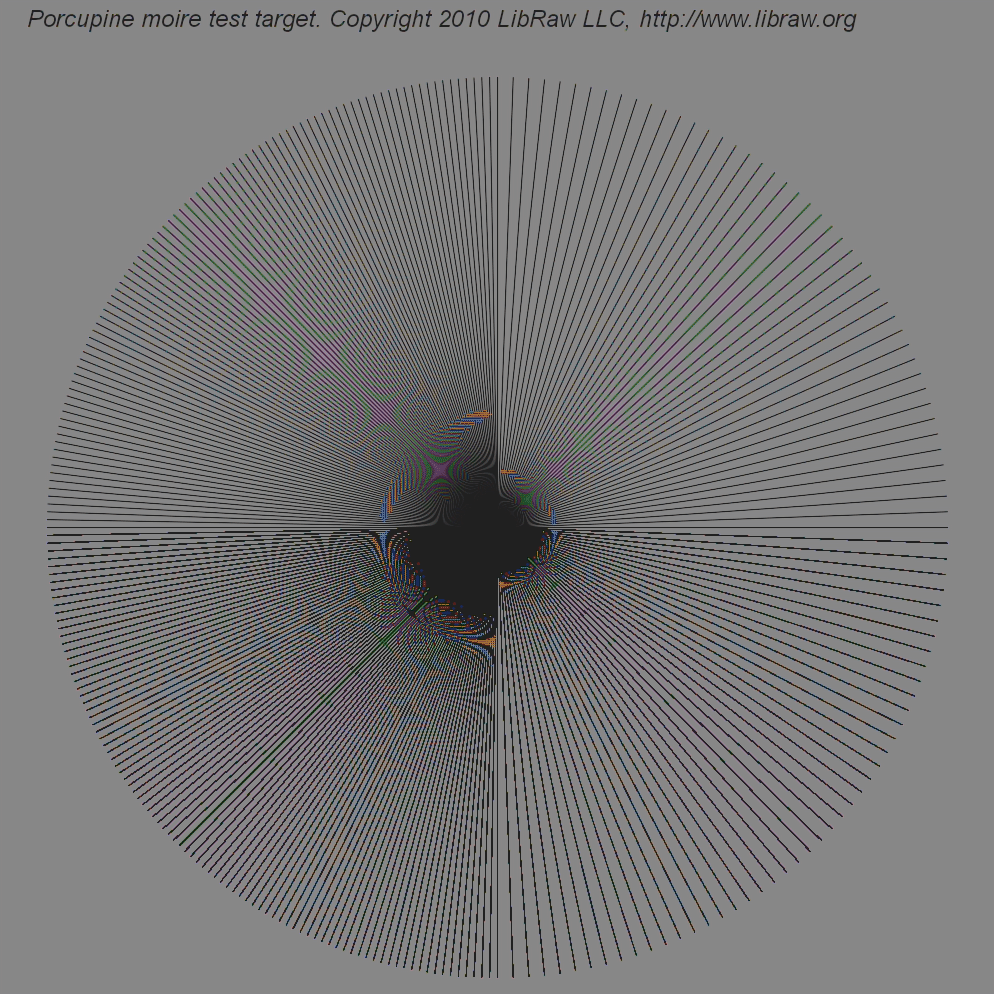
|

|
| Размытая мишень | |
|---|---|
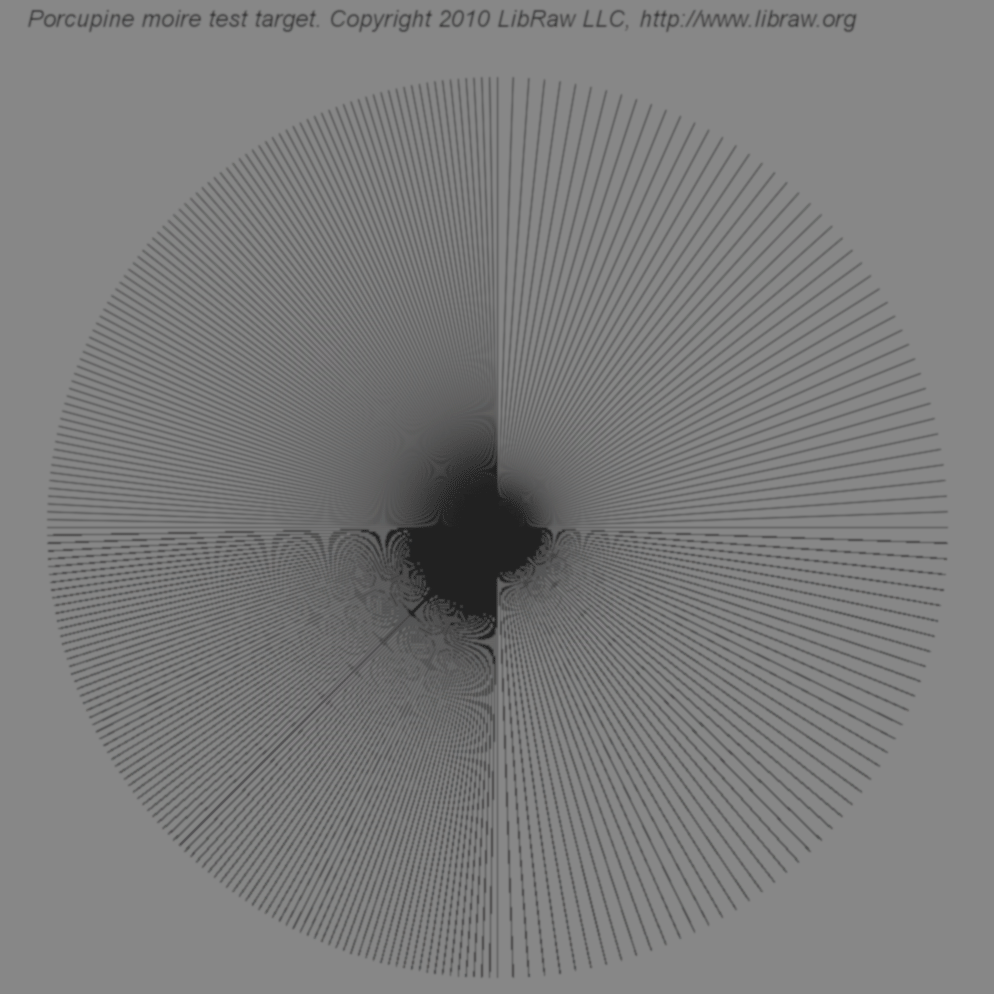
|
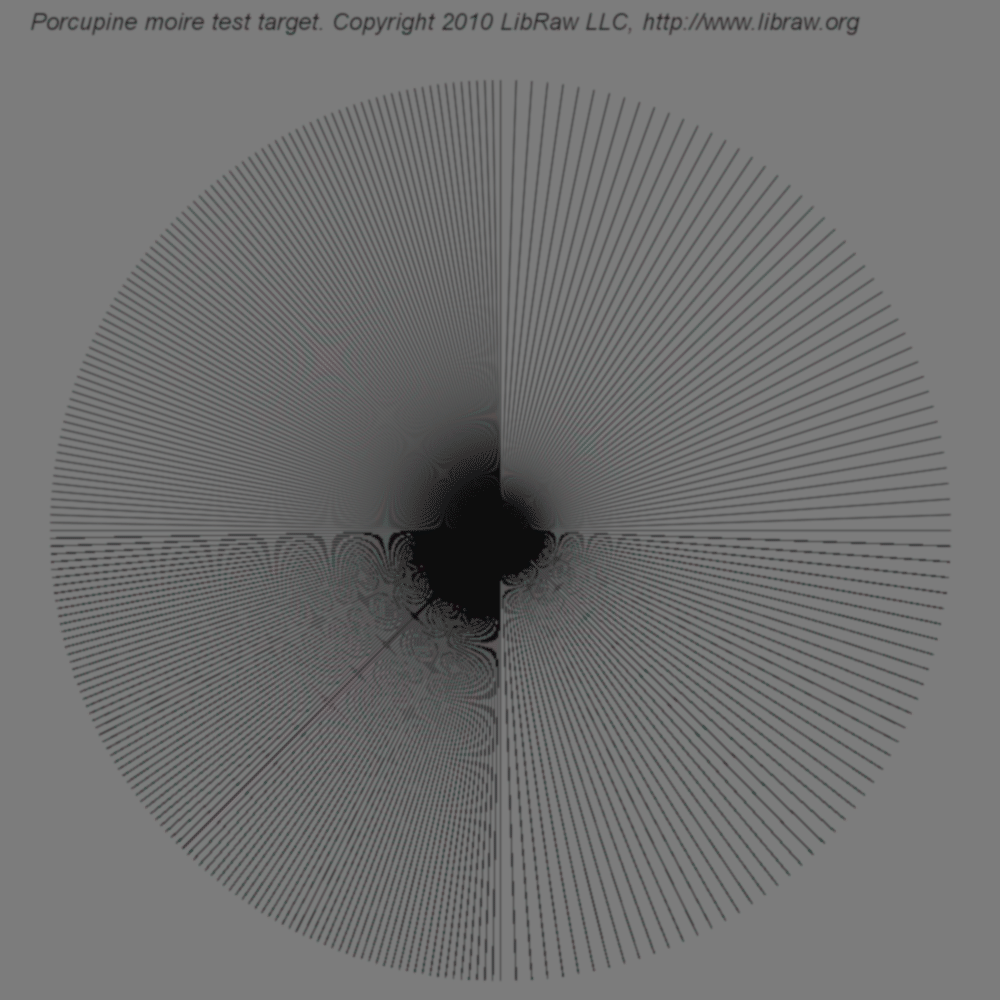
|
Как видно из примеров, артефактов при обработке с плавающей точкой образуется меньше, а разрешение результата, наоборот, больше.
Похоже, что время, которое тратится на стадии обработки на очистку изображения и получение большей детальности, можно было бы с большей пользой истратить на более чистый алгоритм демозаики. Разница во времени двух видов (автоматической!) обработки не превышает нескольких секунд, это существенно меньше времени, которое придется потратить на (ручное!) редактирование изображения для приближения к такому же результату. Попробуйте сами!
Comments
Плавающая точка против целочисленных вычислений.
Приведённые иллюстрации хорошо показывают недостаточность точности целочисленных вычислений. Но пропущен очень важный момент: не указана разрядность целого числа. На самом деле, компьютер работает только с целыми числами. В случае с плавающей точкой он вынужден оперировать с целым набором целых чисел, вместо одного. Это медленно, что справедливо отмечено в статье. Но при этом не упомянут ещё другой недостаток. Массивы данных с плавающей точкой занимают гораздо больше компьютерной памяти, чем массивы целых чисел. Для ускорения вывода графики на экран частенько требуется буферизация, т.е. приходится держать в памяти несколько вариантов изображений. При этом чрезвычайно важна их компактность.
Вообще, я не могу понять, почему точности целого числа может не хватать в любых вычислениях? Все компьютеры сейчас, как минимум 32-битные, т.е. процессор в любом случае оперирует набором из 32 бит, даже когда из них используется только один :). По крайней мере, работа с 32-битными целыми ничуть не медленнее, чем с меньшей разрядностью. Понятно, что 8 бит для обработки изображений мало, но как может не хватать 32 бита, мне не понятно. На самом деле, можно работать и с 64-битными целыми числами, если будет хоть один стимул для этого.
В целых числах вычисления быстрее, память расходуется экономней. Требуется только определить оптимальную разрядность представления целого числа. В целых числах программировать труднее. Я бы сказал, что программирование в действительных числах вместо целых может быть полезно для программистов затрудняющихся оптимизировать свой код на низком уровне. Это удобный способ, чтобы не думать об оптимизации совсем и решить свои проблемы за счёт пользователя, его времени и его компьютерной памяти.
Уважаемый Антон,сегодня,
сегодня, при тотальном распространении процессоров с векторными операциями (SSE, AVX), ваши тезисы не вполне верны:
Так как вы предлагаете пользоваться 32-битными целыми, то об экономии памяти речь, очевидно, не идет. В этом случае никакого выигрыша у целых чисел просто нет. При этом, у плавающей точки одинаковая относительная точность по всему диапазону (вполне достаточная для целей imaging), а у целых - одинаковая абсолютная, избыточная на верхней границе диапазона и, возможно, недостаточная на нижней.
Вопрос производительности плавающей точки/целых чисел я тут, совершенно случайно, исследовал для целей imaging. В конкретном приложении к матричному цветовому преобразованию. Смотрите тут: О legacy и форматах данных и далее там же по тегу Программирование. Вкратце вывод такой: самые быстрые реализации (этого конкретного алгоритма) будут или с haddps, или с dpps, а этих операций для целых чисел процессор просто не поддерживает. И эти реализации получаются в 7 раз быстрее того, что делает C-компилятор для целых чисел.
А знаете, возразить я сейчас
А знаете, возразить я сейчас не сумею. Вы ссылаетесь на код на С, а как раз его синтаксисом я не владею. Быстрые вещи писал на Паскале, используя ассемблерные вставки для часто исполняемых функций. В принципе, это проверяется. В код можно поставить таймер, а проблемные участки для большей точности ещё и в цикл загнать. Обычно оптимизировал скорость так.
Отвлекаясь от возможностей конкретных процессоров, существует оптимальная разрядность для любых вычислений. Избыточная точность - это лишние вычисления. Плавающая точка это и есть избыточное решение на все случаи жизни. Хотя, кажется и в С есть выбор разрядности для плавающей точки. Но малые разрядности всё равно обрабатываются в то же число тактов, что и большие, естественные для процессора.
Ну смотрите что получается:
Ну смотрите что получается:
- 16-битных целых, в-общем, маловато, не хватает точности при многостадийной обработке. 16-битных плавающих хватило бы (при логарифмическом кодировании), но процессор такие данные не поддерживает, а софтверная поддержка будет медленной.
- 24-битных целых процессор не поддерживает, см. выше про библиотеки.
- 32-битных целых и 32-битных float - достаточно по точности.
Только вот с 32-битными float современный процессор (если его правильно использовать) работает быстрее, чем с 32-битными целыми.
Вывод: надо работать в плавучке. Никакого выигрыша по скорости/памяти от 32-битных целых нет, а проигрыш (в виде большой относительной ошибки в районе нуля) - есть.
Спасибо. Немного странно, что
Спасибо. Немного странно, что процессор более сложную операцию делает быстрее, чем простую. Но вполне может быть, они заточены на вполне определённый набор операций. Если доберусь когда-нибудь в программировании до этого места, то объясню точно. :)
Вы считаете абсолютное время
Вы считаете абсолютное время работы, исключая многозадачность. При работе со всем набором FPU инструкций (и их порождений), требуются дополнительные приседания по управлению сохранением состояний процессора, что приводит к ухудшению многопоточной обработки как минимум.
Да, несомненно, такая
Да, несомненно, такая проблема есть.
Но практика простая: http://blog.lexa.ru/2011/08/27/o_legacy_i_formatakh_dannykh.html В плавучке на больших данных (я щупал гигабайт) - в разы быстрее, чем с целыми. Да, плавучка написана руками, а целое - компилятором, ну так и что?
Ну тут еще возникает вопрос
Ну тут еще возникает вопрос компилятора :) Современные компиляторы, типа gcc и icc, а в особенности пока еще недоделанный llvm, выдают на гора отлично оптимизированный код под все существующие процессоры, используя все возможности расширения. А вот от компилятора ms или старого gcc такого не дождешься :) К тому же, никуда не деться от кеша процессора, задержек памяти (особенно в мультипотоковом окружении) и прочей радости, которую компилятор старается учитывать, выравнивая структуры и обращения к памяти.
Поэтому я бы не особенно сильно рассчитывал на особенности ассемблера. К примеру, llvm умеет находить всякие самоделки мемсетов и заменять их парой sse инструкций.
Возможно, в случае полностью известных данных можно добиться большего контроля над скоростью. С этим спорить сложно. Узкоспециализированное всегда будет быстрее.
Компиляторы были достаточно
Компиляторы были достаточно свежие и используемые процессоры - знающие. llvm 3 (бета - на момент исследования), gcc 4.6
Проблема компиляторов, а точнее языка C, в том, что для получения векторизованного кода надо
- сделать выравнивание (и сообщить про него компилятору), а это, блин, плохопереносимые конструкции.
- избавиться от pointer aliasing, что в случае с C++ и указателем this вообще не очень возможно, а в остальных местах требует повсеместного втыкания restrict.
Но и в этом случае код не всегда получается таким уж хорошим.
Начиная с Рentium почти все
Начиная с Рentium почти все операции с плавающей точкой собственно FPU - однотактовые, т.е. быстрее целочисленных в 2-3 раза (даже не касаясь SSE и пр). Возможное торможение на каких-либо тестах может быть связано со смешиванием целых/вещественных чисел или особенностями компиляторов (напр. реализацией math)